P
roblem
In a triangle $ABC$, the angle formed by the intersection $E$ of the bisectors of $∠B$ and the exterior angle of $∠C$ is equal to half of $∠A$.
$$ $$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
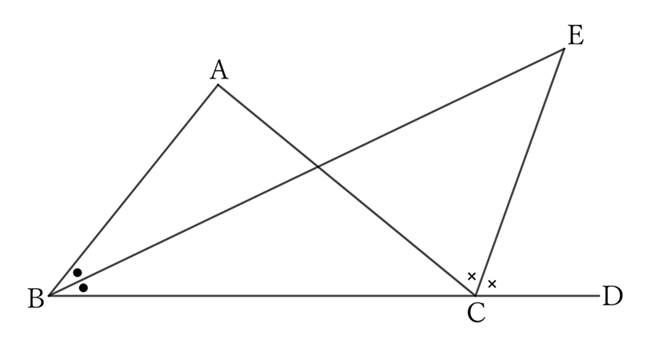
Let $∠A=α$ and $∠B=β$.
Since $∠ACD$ is the exterior angle of $∠C$ in $△ABC$,
$$∠ACD=α+β.$$
Since $EC$ is the bisector of $∠ACD$,
$$∠ECD=\frac{α+β}{2}.$$
However, since $∠ECD$ is the exterior angle of $∠ECB$ in $△EBC$,
$$∠EBC+∠BEC=\frac{α+β}{2}.$$
Since $EB$ is the bisector of $∠B$,
$$∠EBC=\frac{β}{2}.$$
$$∴ \ ∠BEC=\frac{α}{2}.$$
Therefore, $∠BEC$ is half of $∠A$.
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.19
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.19