Problem
In a triangle $ABC$, if $∠B>∠C$, then the bisector $BD$ of $∠B$ is smaller than the bisector $CE$ of $∠C$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
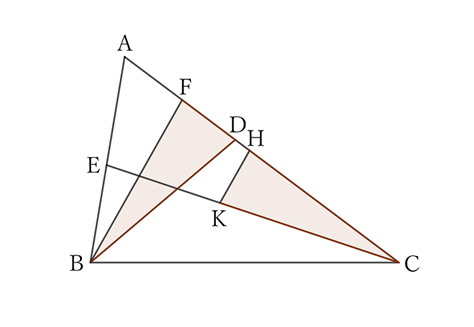
Since $∠B>∠C$,
$$∠ABD>∠ACE.$$
Now, if we take $∠DBF$ equal to $∠ACE$ within $∠ABD$, then in $△FBC$,
$$∠FBC>∠FCB,$$
$$∴ \ FB<FC.$$
Therefore, If we take $CH$ equal to $BD$ on $CF$ and draw a straight line passing through $H$ parallel to $FB$ so that it intersects $CE$ at $K$, then with respect to $△BFD$ and $△CHK$,
$$BF=CH, \quad ∠BFD=∠CHK, \quad and \quad ∠FBD=∠HCK,$$
$$∴ \ △BFD≡△CHK,$$
$$∴ \ KC=BD,$$
$$∴ \ BD<CE.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.19-20