Problem
In a triangle $ABC$, let $D$ be the intersection of the bisector of $∠A$ and the perpendicular bisector of the side $BC$.
When we draw the perpendiculars $DX$ and $DY$ from $D$ to the sides $AB$ and $AC$ or their extensions,
$$AX=AY \qquad and \qquad BX=CY.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
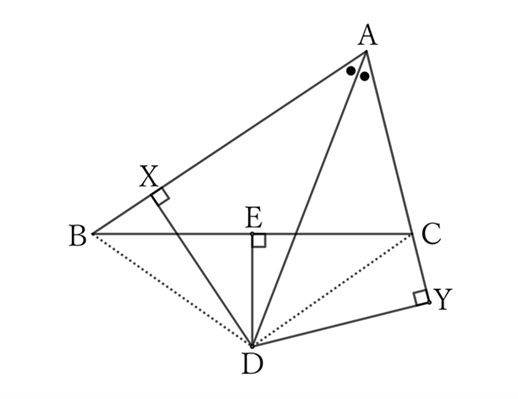
Let $E$ be the midpoint of $BC$.
For the right triangles $ADX$ and $ADY$, they share the side $AD$,
$$∠DAX=∠DAY \qquad and \qquad ∠DXA=∠DXA \ (=∠R),$$
$$∴ \ △ADX≡△ADY,$$
$$∴\ AX=AY.$$
Moreover, regarding the right triangles $DBX$ and $DCY$,
$$DB=DC, \quad DX=DY, \quad and \quad ∠DXB=∠DYC \ (=∠R),$$
$$∴ \ △DBX≡△DCY,$$
$$∴ \ BX=CY.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.21