Problem
Suppose that the side $AB$ of $△ABC$ is one third of the side $AC$.
Drop the perpendicular line $CF$ from $C$ to the bisector $AD$ of $∠A$. Then,
$$AD=DF.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
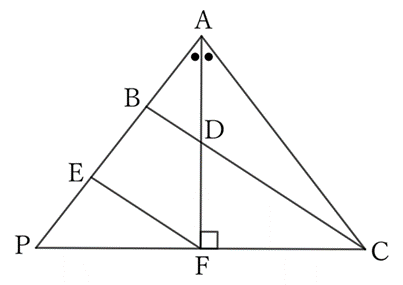
Let $P$ be the intersection of the extensions of $CF$ and $AB$, and draw $EF$ parallel to $BC$.
If $AB=l$,
$$AC=3l.$$
$△APF$ and $△ACF$ share the side $AF$,
$$∠PAF=∠CAF \qquad and \qquad ∠AFP=∠AFC \ (=∠R),$$
$$∴ \ △APF≡△ACF,$$
$$∴ \ AP=3l,$$
$$∴ \ BP=2l.$$
Since $BC∥EF$,
$$△EPF \sim △BPC \qquad and \qquad CP=2FP,$$
$$∴ \ BP=2EP,$$
$$∴ \ BE=EP=l.$$
$$△ABD \sim △AEF \qquad and \qquad AE=2AB=2l,$$
$$∴ \ AF=2AD, $$
$$∴ \ AD=DF.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.21-22