Problem
Let $P$ and $Q$ be the feet of the perpendiculars drawn from $A$ to the bisectors of $∠B$ and $∠C$ of $△ABC$, respectively. Then,
$$PQ=\frac{1}{2} (AB+AC-BC).$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
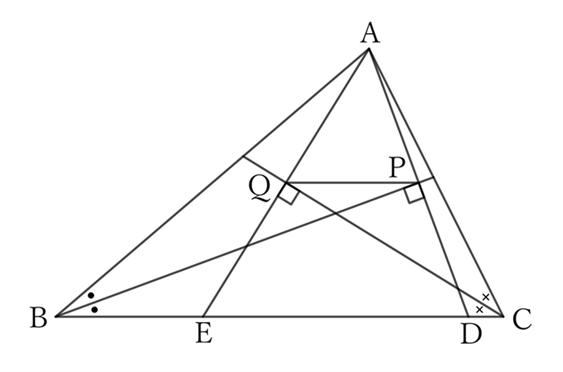
Let the intersections of the extensions of $AP$ and $AQ$ and the side $BC$ be $D$ and $E$, respectively.
$△ABP$ and $△DBP$ share the side $BP$,
$$∠ABP=∠DBP \qquad and \qquad ∠BPA=∠BPD \ (=∠R),$$
$$∴ \ △ABP≡△DBP,$$
$$∴ \ AB=DB \qquad and \qquad AP=DP.$$
$△ACQ$ and $△ECQ$ share the side $CQ$,
$$∠ACQ=∠ECQ \qquad and \qquad ∠CQA=∠CQE \ (=∠R),$$
$$∴ \ △ACQ≡△ECQ,$$
$$∴ \ AC=EC \qquad and \qquad AQ=EQ.$$
Then, $△ADE$ and $△APQ$ share the angle $∠EAD \ (=∠QAP)$,
$$AD∶AP=2∶1 \qquad and \qquad AE∶AQ=2∶1,$$
$$∴ \ △ADE \sim △APQ,$$
$$∴ \ DE∶PQ=2∶1,$$
$$∴ \ PQ=\frac{1}{2} DE.$$
However,
$$DE=DB+EC-BC,$$
$$∴ \ DE=AB+AC-BC,$$
$$∴ \ PQ=\frac{1}{2} (AB+AC-BC).$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.22