Problem
The feet $P, \ Q, \ R$, and $S$ of the perpendiculars drawn from the vertex $A$ of $△ABC$ to the bisectors of the interior and exterior angles of the vertices $B$ and $C$ are on the same line.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
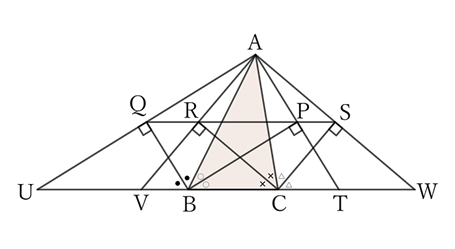
Let the intersections of the extensions of $AP, \ AQ, \ AR$ and $AS$ with the straight line $BC$ be $T, \ U, \ V$ and $W$, respectively.
Then, $△BAP$ and $△BTP$ share the side $BP$,
$$∠ABP=∠TBP \qquad and \qquad ∠BPA=∠BPT \ (=∠R),$$
$$∴ \ △BAP≡△BTP,$$
$$∴ \ AP=TP.$$
Thus, $P$ is the midpoint of $AT$.
Similarly, $Q, \ R$ and $S$ are the midpoints of $AU, \ AV$ and $AW$, respectively.
Therefore, $P, \ Q, \ R$ and $S$ are on the same straight line parallel to the straight line $BC$.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.23