Problem
Is the following statement correct ?
Let the line passing through the midpoint $M$ of the side $AB$ of $△ABC$ intersect with the point $N$ on the side $AC$.
In this case, if $MN=\frac{1}{2} BC$, then
$$MN∥BC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
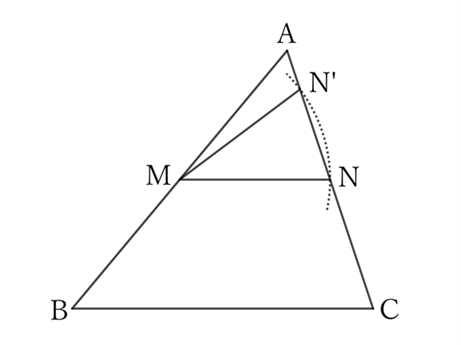
If $N$ is the midpoint of $AC$, $△ABC$ and $△AMN$ share $∠BAC \ (=∠MAN)$,
$$AM=\frac{1}{2} AB \qquad and \qquad AN=\frac{1}{2} AC,$$
$$∴ \ △ABC \sim △AMN,$$
$$∴ \ MN=\frac{1}{2} BC.$$
Then,
$$∠AMN=∠ABC,$$
$$∴ \ MN∥BC.$$
However, if you draw a circle with radius $\frac{1}{2} BC$ centered on $M$, it will generally intersect with the side $AC$ at another point $N’$ in addition to $N$. Then,
$$MN’=\frac{1}{2} BC \qquad but \qquad ∠AMN’≠∠ABC,$$
$$∴ \ MN’∦BC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.24.