Problem
Let $D$ be the midpoint of the side $AB$ of $△ABC$.
If a circle with radius $\frac{1}{2} BC$ centered on $D$ is drawn, prove that it intersects with $AC$ at one or two points, and determine the conditions for there to be only one point of intersection.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
As shown in the problem $0101$, if a circle with a radius of $\frac{1}{2} BC$ is drawn with $D$ as its center, it will generally intersect $AC$ at another point $E’$, in addition to the midpoint $E$ of $AC$.
When a circle with a radius of $\frac{1}{2} BC$ centered on $D$ intersects $AC$ at only one point, it is either when it is tangent to $AC$ at $E$, or when the other point is on the extension of $AC$ (or $CA$).
$(1)$ If the circle is tangent to $AC$ at $E$

Then,
$$∠C=∠R.$$
$(2)$ When $E’$ is on the extension of $AC$
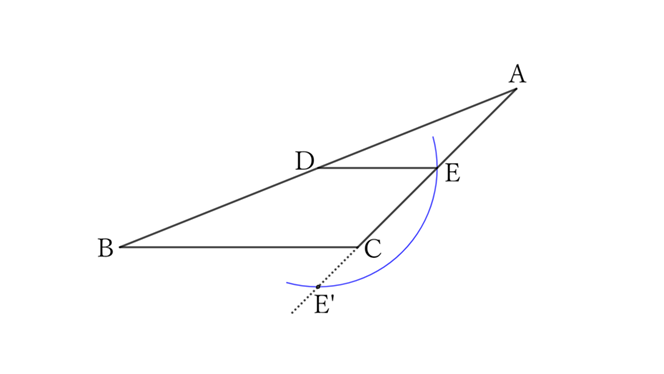
Then,
$$AD>DE>DC,$$
$$∴ \ AD>\frac{1}{2} BC>DC.$$
$(3)$ If $E’$ is an extension of $CA$
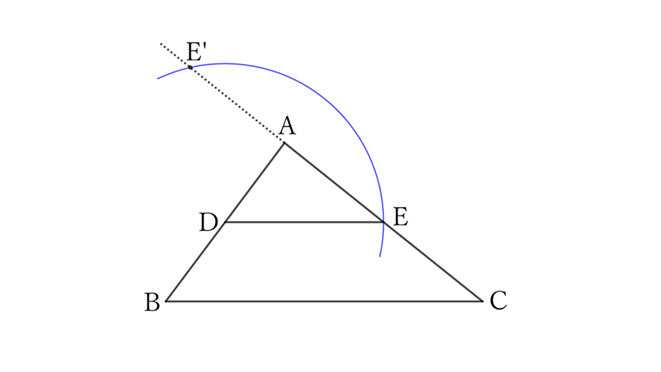
Then,
$$AD<DE<DC,$$
$$∴ \ AD<\frac{1}{2} BC<DC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.24.