Problem
In $△ABC$, let $D$ be the midpoint of $AB$. Then, the length of the line segment connecting $D$ and the midpoint $E$ of $AC$ is $\frac{1}{2} BC$.
State the converse of this theorem and determine the conditions for it to hold.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
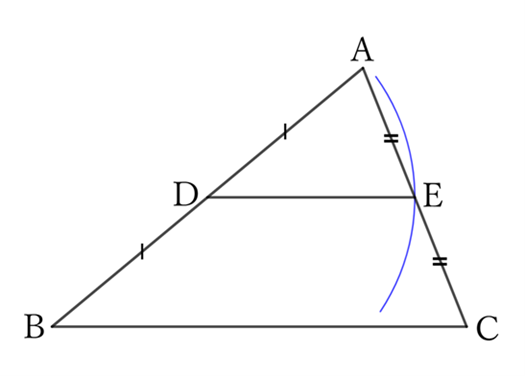
If you draw a line segment $DE$ with a length of $\frac{1}{2} BC$ from the midpoint $D$ of $AB$ to $AC$, $E$ is the midpoint of $AC$.
As we saw in the problem $0102$, the conditions for this to be true are
$$∠C=∠R, \qquad AD>\frac{1}{2} BC>DC, \qquad or \qquad AD<\frac{1}{2} BC<DC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.25.