Problem
The points $B$ and $C$ are on the same side of the line $XY$, and $A$ is on the opposite side.
When the sum of the distances from $B$ and $C$ to $XY$ is equal to the distance from $A$ to $XY$, $XY$ passes through the center of gravity of $△ABC$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
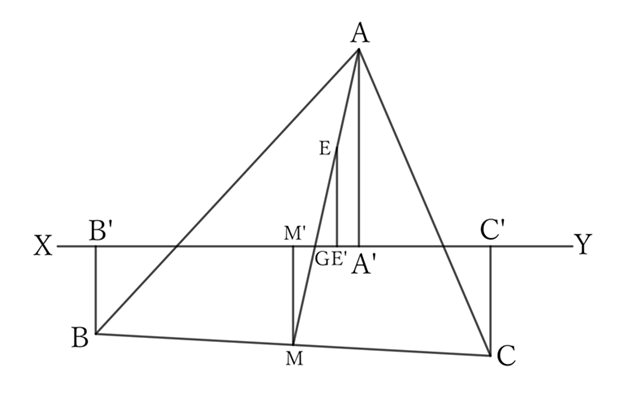
Take the midpoint $M$ on $BC$.
Let the intersection point of the median $AM$ and the line $XY$ be $G$, and the midpoint of $AG$ be $E$.
Furthermore, let the feet of the perpendiculars drawn from $M$ and $E$ to $XY$ be $M’$ and $E’$, respectively. Then,
$$BB’+CC’=2MM’.$$
From the problem statement,
$$AA’=BB’+CC’,$$
$$∴ \ AA’=2MM’.$$
Since $E$ is the midpoint of $AG$,
$$AA’=2EE’,$$
$$∴ \ MM’=EE’,$$
$$∴ \ EG=GM,$$
$$∴ \ AG∶GM=2∶1.$$
In other words, $G$ divides the median $AM$ into $2∶1$.
Therefore, $G$ is the center of gravity of $△ABC$, and the line $XY$ passes through it.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.26.