Problem
In $△ABC$, extend the median $AM$ so that $MD=BC$.
If $∠AMC=60°$, then
$$BD⊥BC.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
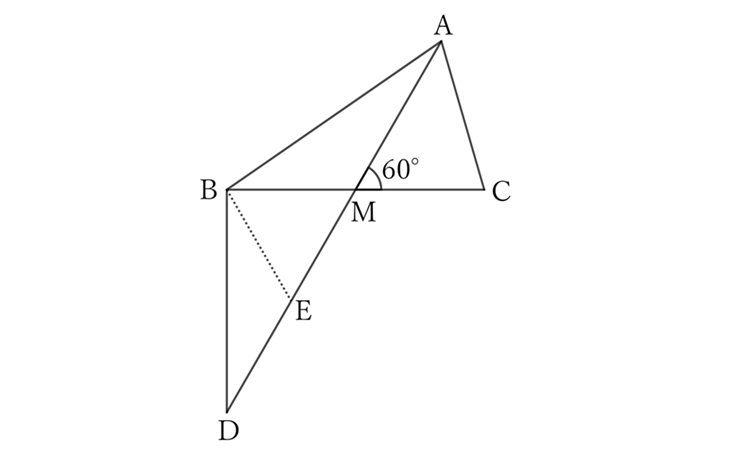
Taking the midpoint $E$ of $MD$,
$$ME=MB \qquad and \qquad ∠BME=60°.$$
Thus, $△MBE$ is an equilateral triangle, and
$$∠MBE=60°. \qquad [1]$$
Moreover,
$$ME=ED \qquad and \qquad ME=EB,$$
$$∴ \ EB=ED.$$
Therefore, $△EBD$ is an isosceles triangle with $E$ as its vertex, and since $∠BED=120°$,
$$∠EBD=30°. \qquad [2]$$
From $[1]$ and $[2]$,
$$∠MBD=∠MBE+∠EBD=60°+30°=90°,$$
$$∴ \ BD⊥BC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.27.