Problem
If the midpoint of the side $BC$ of $△ABC$ is $D$ and $∠ABD+∠DAC=∠R$, what type of triangle is $△ABC$ ?
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
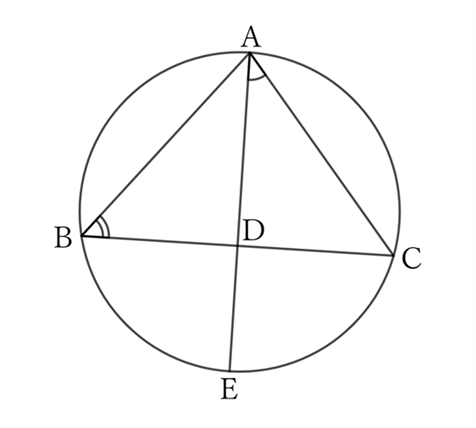
Draw a circle circumscribing $△ABC$, and let $E$ be the point where the extension of the median $AD$ intersects with the circle.
Since $∠ABD+∠DAC=∠R$, we can see that the sum of the arcs $AC$ and $EC$, that is, the arc $AE$, is a semicircle, and the line segment $AE$ is the diameter of the circle.
$D$ is the center of the circle, or at least a point where $AD⊥BC$, and $AB=AC$.
In the end, $△ABC$ is either an isosceles right triangle with $∠A=∠R$, or an isosceles triangle with $AB=AC$.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.28.