Problem
If the vertex of the right angle of a right triangle $ABC$ is $C$ and the midpoint of the hypotenuse $AB$ is $D$, then
$$CD=\frac{1}{2} AB.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
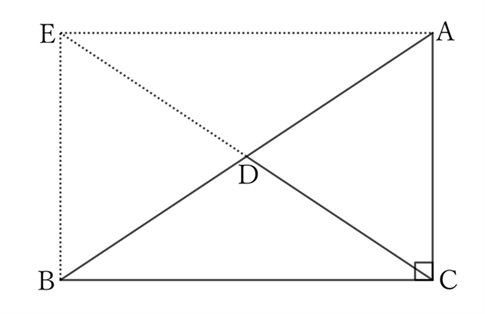
If we extend $CD$ so that $CD=DE$ and take point $E$,
$$AD=DB, \qquad ED=DC \qquad and \qquad ∠C=∠R.$$
Therefore, $ABCD$ is a rectangle and
$$AB=CE.$$
However,
$$CD=\frac{1}{2} CE,$$
$$∴ \ CD=\frac{1}{2} AB.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.28.