Problem
In a triangle $ABC$ with right angle $∠B$, when $∠C=60°$ and $∠A=30°$, the hypotenuse $AC$ is twice the length of the side $BC$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
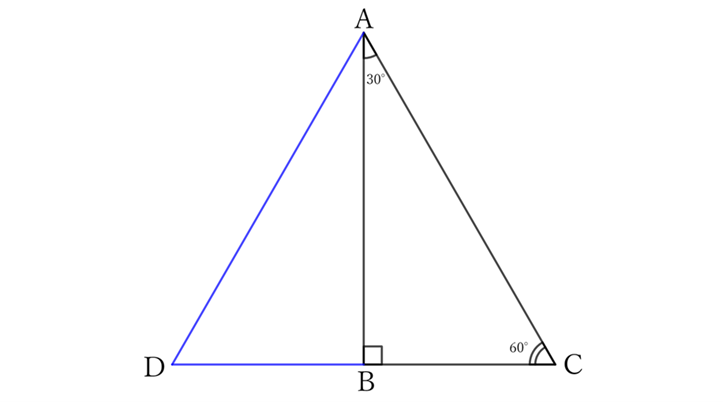
Extend $CB$ and take point $D$ such that $CB=DB$.
Then since $△ABC$ and $△ABD$ share the side $AB$, $BC=BD$ and $∠ABC=∠ABD=∠R$,
$$△ABC≡△ABD,$$
$$∴ \ ∠BAC=∠BAD=30°,$$
$$∴ \ ∠CAD=60°.$$
Therefore, $△ACD$ is an equilateral triangle, $AC$ is one side, and $BC$ is half of one side. Thus,
$$BC=\frac{1}{2} AC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.28.