Let $D$ be the foot of the perpendicular line drawn from the right-angled vertex $A$ of a rectangular triangle $ABC$ to the hypotenuse $BC$.

Then, the sum of the diameters of the inscribed circles of $△ABC, \ △ABD$ and $△ACD$ is equal to twice the length of $AD$.

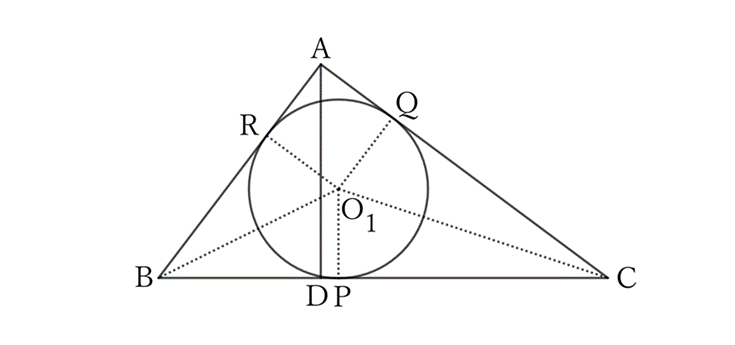
Let $O_1$ and $d_1$ be the center and diameter of the circle inscribed in the right triangle $ABC$, respectively, and let $P, \ Q$ and $R$ be the points of contact of that circle with $BC, \ CA$ and $AB$, respectively.

Since $△O_1 BR≡△O_1 BP$,

$$BR=BP,$$

$$∴ \ AB-\frac{1}{2} d_1=BP.$$

Since $△O_1 QC≡△O_1 PC$,

$$CQ=CP,$$

$$∴ \ CA-\frac{1}{2} d_1=CP.$$

Since $BC=BP+CP$,

$$BC=AB+CA-d_1,$$

$$∴ \ d_1=AB+CA-BC.$$

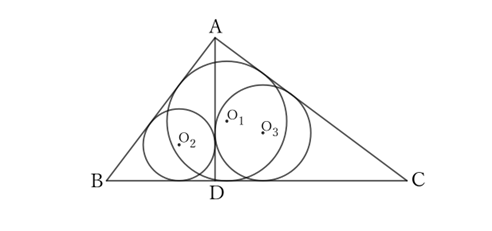
Similarly, let the center and diameter of the inscribed circle of $△ABD$ be $O_2$ and $d_2$, respectively, and those of the inscribed circle of $△ACD$ be $O_3$ and $d_3$.

Then,

$$d_2=AD+DB-AB \qquad and \qquad d_3=AD+DC-CA,$$

$$\begin{eqnarray} ∴ \ d_1+d_2+d_3=(AB+CA-BC)+(AD+DB-AB)+(AD+DC-CA) \\ =-BC+2AD+DB+DC=2AD. \qquad (∵ DB+DC=BC) \end{eqnarray}.$$

$ $