In a rectangular triangle $ABC$ with $∠A$ as a right angle, if $D$ and $E$ are placed on the hypotenuse $BC$ such that $BD=AB$ and $CE=AC$, then $∠CAD$ and $∠BAE$ are equal to half of $∠B$ and $∠C$ respectively.

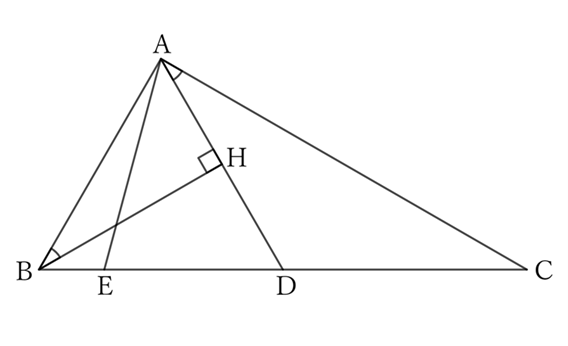
Let $H$ be the foot of the perpendicular line from $B$ to $AD$.

First,

$$∠CAD+∠DAB \ (=∠A) \ =∠R.$$

However, for $△ABH$,

$$∠ABH+∠HAB=∠R,$$

$$∠DAB=∠HAB,$$

$$∴ \ ∠ABH+∠DAB=∠R,$$

$$∴ \ ∠CAD=∠ABH.$$

Then, since $BD=AB$, $△BAD$ is an isosceles triangle with $B$ as its vertex.

Thus, $BH$ is the bisector of $∠B$.

$$∴ \ ∠ABH=\frac{1}{2}∠B,$$

$$∴ \ ∠CAD=\frac{1}{2}∠B.$$

Next, since $CE=AC$, $△CAE$ is C is an isosceles triangle with $C$ as its vertex. Therefore,
$$∠CAE=∠CEA=∠R-\frac{1}{2}∠C.$$

Then,
$$∠A=∠BAE+∠CAE=∠R,$$
$$∴ \ ∠BAE+∠R-\frac{1}{2}∠C=∠R,$$
$$∴ \ ∠BAE=\frac{1}{2}∠C.$$

$ $