In a rectangular triangle $ABC$ with $B$ as the right-angled vertex, if $D$ and $E$ are the feet of perpendicular lines drawn from $A$ to the bisectors of $∠C$ and its exterior angle, then $DE$ bisects $AB$ vertically.

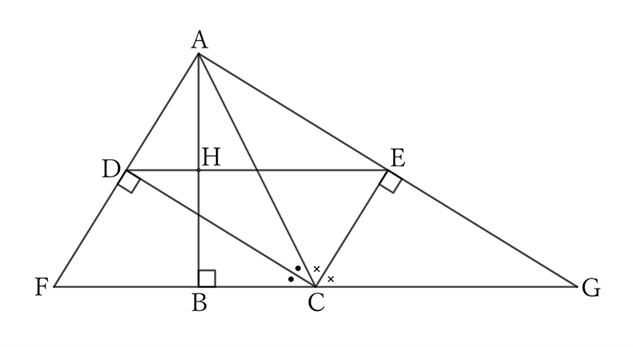
Extend both ends of $BC$ and let F and G be the points where they intersect with the extensions of $AD$ and $AE$, respectively, and $H$ be the point where $DE$ intersects with $AB$.

$△ACD$ and $△FCD$ share the side $CD$,

$$∠ACD=∠FCD \qquad and \qquad ∠CDA=∠CDF \ (=∠R),$$

$$∴ \ △ACD≡△FCD,$$

$$∴ \ DA=DF.$$

Therefore, $D$ is the midpoint of $AF$.

Similarly, $△ACE$ and $△GCE$ share the side $CE$,

$$∠ACE=∠GCE \qquad and \qquad ∠CEA=∠CEG \ (=∠R),$$

$$∴ \ △ACE≡△GCE,$$

$$∴ \ EA=EG.$$

Therefore, $E$ is the midpoint of $AG$.

Since $△AFG$ is a right triangle with $∠GAF=∠R$, the line passing through the midpoints $D$ and $E$ of the two sides $AF$ and $AG$ that make up the right angle passes through the midpoint $H$ of the perpendicular line $AB$ from $A$ to $FG$.

Since the quadrilateral $ADCE$ is a rectangle,

$$∠CAE=∠EDC.$$

Moreover,

$$∠CAE=∠CGE,$$

$$∴ \ ∠CGE=∠EDC,$$

$$∴ \ CG∥DE.$$

Since $BC⊥AB$,

$$CG⊥AB,$$

$$∴ DE⊥AB.$$

In other words, $DE$ intersects $AB$ perpendicularly and passes through the midpoint $H$ of $AB$.

$ $