Problem
Take a point $D$ inside the isosceles right triangle $ABC$ with $∠C=∠R$, so that $AD=AC$ and $∠CAD=30°$. Then
$$BD=CD.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
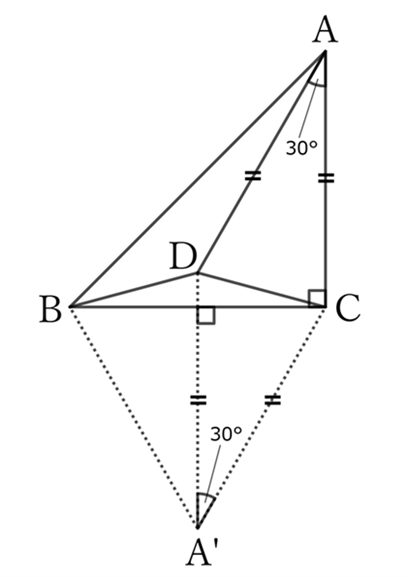
If the point symmetrical to $A$ with respect to $DC$ is $A’$, then
$$∠BCA’=∠ACA’-∠ACB=150°-90°=60°,$$
$$AC=A’ C \qquad and \qquad AC=BC,$$
$$∴ \ A’ C=BC.$$
Therefore, since $△A’ BC$ is an equilateral triangle,
$$A’ B=A’ C \qquad and \qquad ∠BA’ D=∠CA’ D=30°,$$
$$∴ \ △A’ BD≡△A’ CD,$$
$$∴ \ BD=CD.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.31.