Problem
In a triangle $ABC$, if $AB=AC$, then
$$∠B=∠C.$$
And vice versa.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
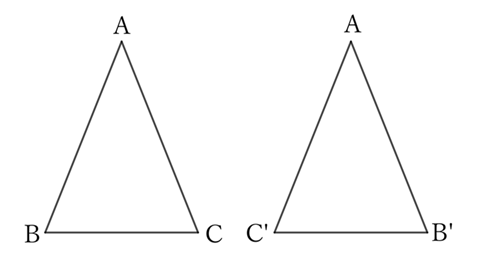
If we turn $△ABC$ over and make it $△AC’ B’$,
$$AB=AC’ \qquad and \qquad AC=AB’, \qquad (∵ \ AB=AC)$$
$$and \qquad BC=C’ B’,$$
$$∴ \ △ABC≡△AC’ B’,$$
$$∴ \ ∠B=∠C’ \qquad and \qquad ∠C=∠B’.$$
However, since $∠B=∠B’$ and $∠C=∠C’$,
$$∠B=∠C.$$
Also, conversely, if $∠B=∠C$,
$$BC=C’ B’, \qquad ∠B=∠C’ \qquad and \qquad ∠C=∠B’,$$
$$∴ \ △ABC≡△AC’ B’,$$
$$∴ \ AB=AC’ \qquad and \qquad AC=AB’.$$
However, since $AB=AB’$ and $AC=AC’$,
$$AB=AC.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.32.