Problem
The straight line connecting the intersection of perpendicular lines drawn from both ends of the base of an isosceles triangle to the vertex bisects the apex angle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
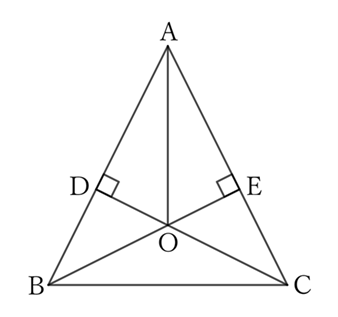
If the intersection point of $BE$ and $CD$ is $O$, then $△ACD$ and $△ABE$ share $∠A$,
$$AC=AB \qquad and \qquad ∠CDA=∠BEA \ (=∠R).$$
Therefore, from the problem $0031$,
$$△ACD≡△ABE,$$
$$∴ \ AD=AE.$$
$△AOD$ and $△AOE$ share the side $AO$,
$$AD=AE \qquad and \qquad ∠ODA=∠OEA \ (=∠R).$$
Therefore, from the problem $0032$,
$$△AOD≡△AOE,$$
$$∴ \ ∠DAO=∠EAO.$$
In other words, the line $AO$ bisects $∠A$.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.32.