If the sum of perpendicular lines $PD$ and $PF$ drawn from any point $P$ on one side of an isosceles triangle $ABC$ with vertex $A$ to the other two sides is equal to the height $AH$, then $△ABC$ is an equilateral triangle.

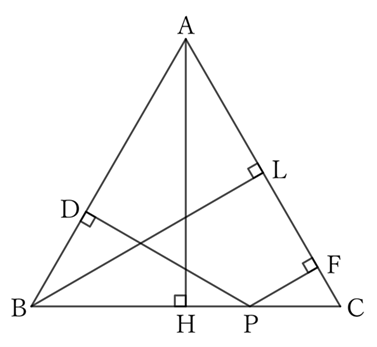
If we drop a perpendicular line $BL$ from $B$ to $AC$, then from the problem $151$,

$$PD+PF=BL.$$

However, from the problem statement,

$$PD+PF=AH,$$

$$∴ \ BL=AH. \qquad [1]$$

Then, regarding $△BCL$ and $ACH$,

$$∠BLC=∠AHC \ (=∠R). \qquad [2]$$

Furthermore,

$$∠LBC=∠R-∠BLC \qquad and \qquad ∠HAC=∠R-∠AHC,$$

$$∴ \ ∠LBC= ∠HAC. \qquad [3]$$

From $[1],\ [2]$ and $[3]$,

$$△BCL≡△ACH,$$

$$∴ \ BC=AC,$$

$$∴ \ AB=BC=AC.$$

Therefore, $△ABC$ is an equilateral triangle.

(2) The case where $P$ is on the side $AC$ (or $AB$)

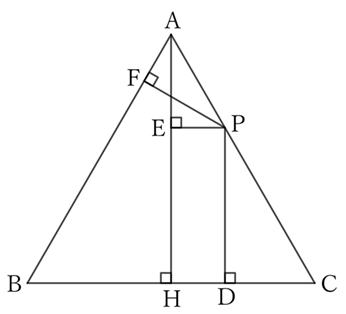
If we draw a perpendicular line $PE$ from $P$ to the height $AH$,

$$PD=EH. \qquad [4]$$

However, from the problem statement,

$$PD+PF=AH. \qquad [5]$$

From $[4]$ and $[5]$,

$$EH+PF=AH,$$

$$∴ \ PF=AE.$$

$△APF$ and $△PAE$ share the side $AP \ (=PA)$,

$$PF=AE \qquad and \qquad ∠AFP=∠PEA \ (=∠R),$$

$$∴ \ △APF≡△PAE,$$

$$∴ \ ∠PAF \ (=∠A) \ =∠APE \ (=∠C).$$

However,

$$∠B=∠C,$$

$$∴ \ ∠A=∠B=∠C.$$

Therefore, $△ABC$ is an equilateral triangle.

$ $