The difference between the perpendicular lines $PQ$ and $PR$ drawn from any point $P$ on the extension of the base $BC$ of an isosceles triangle $ABC$ to the sides $AB$ and $AC$ (or their extensions) is constant.

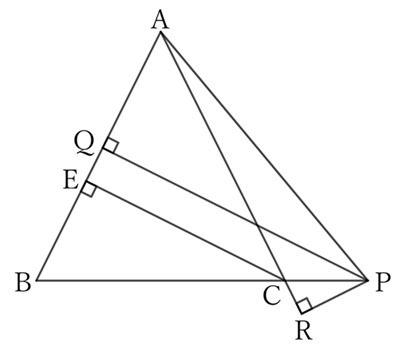
If we draw a perpendicular line $CE$ from $C$ to $AB$ and connect $A$ and $P$,
$$△ABC=\frac{1}{2}×AB×CE, \qquad [1]$$
$$△ACP=\frac{1}{2}×AC×PR, \qquad [2]$$
$$△ABP=\frac{1}{2}×AB×PQ. \qquad [3]$$
However, since $AB=AC$,
$$△ACP=\frac{1}{2}×AB×PR. \qquad [2]’$$
Note that

$$△ABP-△ACP=△ABC.$$

Thus, from $[1], \ [2]’$ and $[3]$,
$$\frac{1}{2}×AB×PQ-\frac{1}{2}×AB×PR=\frac{1}{2}×AB×CE,$$
$$∴ \ PQ-PR=CE.$$
Therefore, wherever $P$ is on the extension of $BC$, $PQ-PR$ is always equal to $CE$.

$ $