Problem
If there are three points $D, \ E$ and $F$ on each side of an equilateral triangle $ABC$ such that $AD=BE=CF$, then the triangle $DEF$ is also an equilateral triangle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
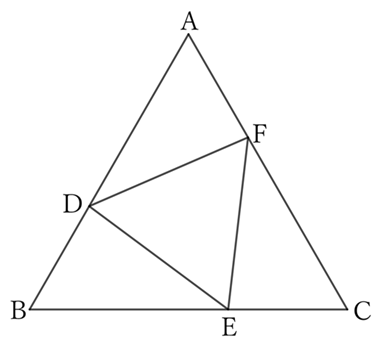
Since $△ABC$ is an equilateral triangle,
$$AB=BC=CA.$$
From the problem statement,
$$AD=BE=CF,$$
$$∴ \ BD=CE=AF.$$
Regarding $△ADF, \ △BED$, and $△CFE$,
$$AD=BE=CF, \qquad AF=BD=CE\qquad and \qquad ∠DAF=∠EBD=∠FCE \ (=60°),$$
$$∴ \ △ADF≡△BED≡△CFE,$$
$$∴ \ DF=DE=EF.$$
Therefore, a triangle $DEF$ is an equilateral triangle.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, pp.35-36.