Problem
Take three points $D, \ E$ and $F$ on each side of a triangle $ABC$ such that $AD=BE=CF$.
Then, if the triangle $DEF$ is an equilateral triangle, $△ABC$ is also an equilateral triangle.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
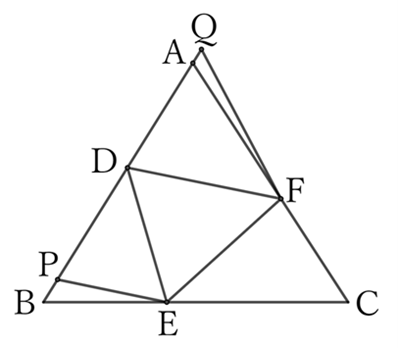
If any two sides of $AB, \ BC$ and $AC$, for example $AB$ and $AC$, are equal, then
$$AF=BD. \qquad (∵ CF=AD)$$
Furthermore,
$$AD=BE \qquad and \qquad FD=DE,$$
$$∴ \ △ADF≡△BED,$$
$$∴ \ ∠A=∠B.$$
However, since we are assuming that $AB=AC$,
$$∠B=∠C,$$
$$∴ \ ∠A=∠B=∠C.$$
Therefore, $△ABC$ is an equilateral triangle.
If $∠A, \ ∠B$, and $∠C$ are not equal, then at least one of the three is greater than $60°$ and another is less than $60°$.
Thus, we will assume that
$$∠A>60° \qquad and \qquad ∠B<60°.$$
Take points $P$ and $Q$ on $BA$ and its extension such that $∠DPE=∠AQF=60°$.
Then since the sum of the interior angles of $△DPE$ is equal to $∠ADF+∠FDE+∠EDP$, and $∠DPE=60°=∠FDE$,
$$∠DEP=∠ADF.$$
Therefore,
$$∠Q=∠P \ (=60°), \qquad ∠QDF=∠DEP \qquad and \qquad DF=DE,$$
$$∴ \ △QDF≡△PED,$$
$$∴ \ QD=PE. \qquad [1]$$
Since $∠BPE$ is an obtuse angle ($120°$),
$$BE>PE,$$
$$∴ \ BE>QD. \qquad [2]$$
However, by the problem statement,
$$BE=DA.$$
Hence, $[2]$ does not hold.
Therefore, if any two of the three sides of $△ABC$ are equal, the other side is also equal and it becomes an equilateral triangle.
If none of the three sides are equal, this problem does not hold.
Thus, $△ABC$ is definitely an equilateral triangle.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.36.