If equilateral triangles $BCX$ and $CDY$, with the bases $BC$ and $CD$ of a parallelogram $ABCD$, are drawn outside the quadrilateral, then $△AXY$ becomes an equilateral triangle.

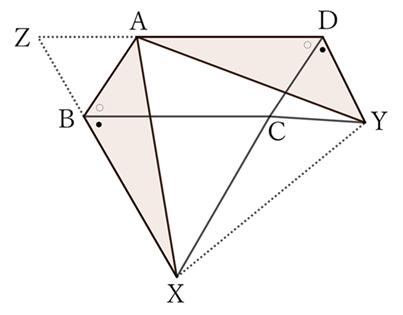
For $△ABX$ and $△YDA$,

$$AB=YD, \qquad BX=DA \qquad and \qquad ∠ABX=∠YDA,$$

$$∴ \ △ABX≡△YDA,$$

$$∴ \ XA=AY. \qquad [1]$$

However, since $ZD∥BC$ and $∠CBX$ and $∠Z$ are corresponding angles, for $△ABX$ and $△YDA$, the angle between corresponding sides $BX$ and $DA$ is

$$∠Z=60°.$$

Therefore, the angle between corresponding sides $AX$ and $YA$ is also

$$∠XAY=60°. \qquad [2]$$

From $[1]$ and $[2]$, $△AXY$ is an equilateral triangle.