Problem
If each side of a triangle $ABC$ is used as base and equilateral triangles $BCD, \ CAE$ and $ABF$ are constructed outside the triangle, then the lengths of line segments $AD, \ BE$ and $CF$ are equal.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
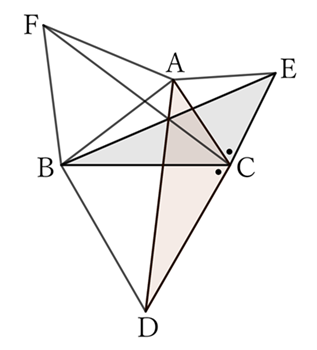
For $△ACD$ and $△ECB$,
$$AC=EC \qquad and \qquad CD=CB. \qquad [1]$$
Furthermore,
$$∠ACD=∠ACB+∠BCD, \qquad ∠ECB=∠ECA+∠ACB$$
$$and \qquad ∠BCD=ECA \ (=60°),$$
$$∴ \ ∠ACD=∠ECB. \qquad [2]$$
From $[1]$ and $[2]$,
$$△ACD≡△ECB,$$
$$∴ \ AD=EB. \qquad [3]$$
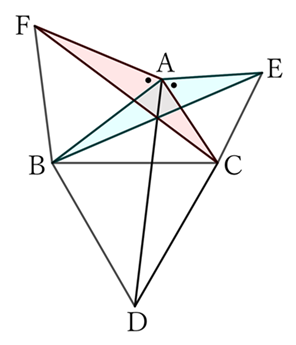
For $△ABE$ and $△AFC$,
$$AB=AF \qquad and \qquad EA=CA. \qquad [4]$$
Furthermore,
$$∠BAE=∠BAC+∠CAE, \qquad ∠FAC=∠FAB+∠BAC$$
$$and \qquad ∠CAE=∠FAB \ (=60°),$$
$$∴ \ ∠BAE=∠FAC. \qquad [5]$$
From $[4]$ and $[5]$,
$$△ABE≡△AFC,$$
$$∴ \ BE=FC. \qquad [6]$$
From $[3]$ and $[6]$,
$$AD=BE=CF.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.37.