Problem
Let $D$ and $E$ be points on sides $BC$ and $CA$ respectively of a triangle $ABC$, such that $$BD=\frac{1}{2} DC \qquad and \qquad CE=EA.$$
Then $AD$ bisects $BE$.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
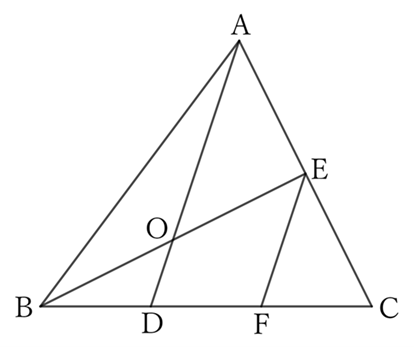
Let $F$ be the midpoint of $DC$, and $O$ be the intersection of $AD$ and $BE$.
Then, $△ACD$ and $△ECF$ share $∠C$,
$$AC∶EC=2∶1 \qquad and \qquad CD∶CF=2∶1,$$
$$∴ \ △ACD≡△ECF,$$
$$∴ \ AD∥EF.$$
$△BEF$ and $△BOD$ share $∠EBF \ (=∠OBD)$,
$$BF∶BD=2∶1 \qquad and \qquad OD∥EF,$$
$$∴ \ △BEF≡△BOD,$$
$$∴ \ BE∶BO=2∶1,$$
$$∴ BO∶OE=1∶1.$$
In other words, $AD$ bisects $BE$.
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.38.