(1) Let $M$ be the midpoint of the line segment $AB$.

      Connect $M$ to a point $P$ outside this line.

      If $MP<MA$, which is $∠APB$ an acute or obtuse angle?

      Furthermore, what if $MP>MA$?

(2) Prove that the midpoint of the hypotenuse of a right triangle is equidistant from the three vertices.

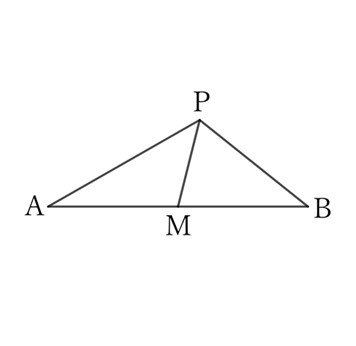
For $△MAP$,

$$MP<MA.$$

Thus, from the problem $0038$,

$$∠MPA>∠MAP.$$

Similarly, for $△MBP$,

$$MP<MB \qquad (∵ \ MA=MB),$$

$$∠MPB>∠MBP.$$

Therefore,

$$∠MPA+∠MPB>∠MAP+∠MBP,$$

$$∴ \ ∠APB>∠MAP+∠MBP,$$

$$∴ \ ∠APB>∠A+∠B.$$

In that case, if $∠APB≤90°,$

$$∠A+∠B<90°,$$

$$∴ \ ∠APB+∠A+∠B<180°.$$

However, then since the sum of the interior angles of $△PAB$ is less than $180°$, a contradiction arises.

Thus,

$$∠APB>90°.$$

In other words, when $MP<MA$, $∠APB$ is an obtuse angle.

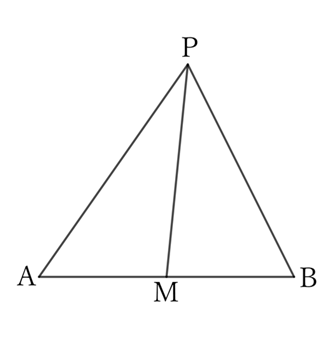
For $△MAP$,

$$MP>MA.$$

Thus, from the problem $0038$,

$$∠MPA<∠MAP.$$

Similarly, for $△MBP$,

$$MP>MB \qquad (∵ \ MA=MB),$$

$$∠MPB<∠MBP.$$

Therefore,

$$∠MPA+∠MPB<∠MAP+∠MBP,$$

$$∴ \ ∠APB<∠MAP+∠MBP,$$

$$∴ \ ∠APB<∠A+∠B.$$

In that case, if $∠APB≥90°$,

$$∠A+∠B>90°,$$

$$∴ \ ∠APB+∠A+∠B>180°.$$

However, then since the sum of the interior angles of $△PAB$ is more than $180°$, a contradiction arises;

$$∴ \ ∠APB<90°.$$

In other words, when $MP>MA$, $∠APB$ is an acute angle.

(2)

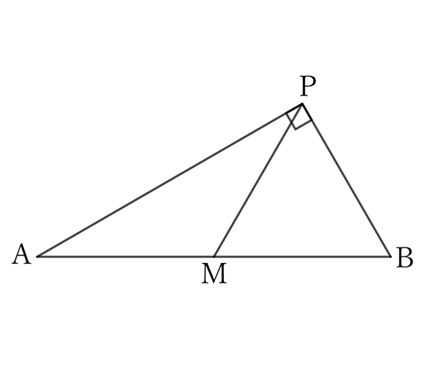
Let $M$ be the midpoint of $AB$ and $∠APB=90°$.

If $MP<MA \ (=MB)$, then from $(1)$ above,

$$∠APB>90°.$$

This contradicts the condition $∠APB=90°$.

Similarly, if $MP>MA \ (=MB)$,

$$∠APB<90°.$$

This also contradicts the condition $∠APB=90°$.

Therefore, $MP=MA=MB$ must be true.

$ $