From the midpoints $P$ and $Q$ of sides $AB$ and $AC$ of triangle $ABC$, draw perpendicular lines $PD$ and $QE$ to the outside of the triangle such that

$$PD=\frac{1}{2} AB \qquad and \qquad QE=\frac{1}{2} AC.$$

Then, $DM$ and $EM$, which connect $D$ and $E$ to the midpoint $M$ of side $BC$, are equal and perpendicular.

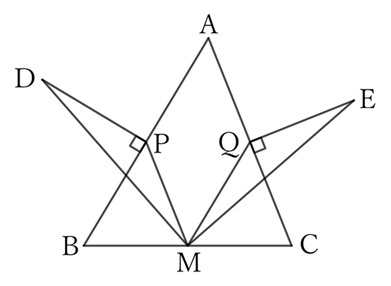
$△ABC$ and $△PBM$ share $∠ABC \ (=∠PBM)$,

$$AB∶PB=2∶1 \qquad and \qquad BC∶BM=2∶1,$$

$$∴ \ △ABC∼△PBM,$$

$$∴ \ ∠BAC=∠BPM,$$

$$∴ \ AQ∥PM.$$

$△ABC$ and $△QMC$ share $∠ACB \ (=∠QCM)$,

$$AC∶QC=2∶1 \qquad and \qquad BC∶MC=2∶1,$$

$$∴ \ △ABC∼△QMC,$$

$$∴ \ ∠BAC=∠MQC,$$

$$∴ \ AP∥QM.$$

Therefore, since quadrilateral $APMQ$ is a parallelogram,

$$PM=AQ,$$

$$∴ \ PM=QE. \qquad (∵ AQ=QE)$$

$$AP=QM,$$

$$∴ \ PD=QM. \qquad (∵ AP=PD)$$

$$△PBM≡△QMC,$$

$$∴ \ ∠BPM=∠MQC,$$

$$∴ \ ∠DPM=∠MQE,$$

$$∴ \ △PDM≡△QME,$$

$$∴ \ DM=ME.$$

Furthermore,

$$∠DME=∠DMP+∠PMQ+∠QME,$$

$$∠PMQ=∠BPM \qquad and \qquad ∠QME=∠PDM,$$

$$∴ \ ∠DME=∠DMP+∠BPM+∠PDM$$

$$=∠DMP+(∠DPM-∠DPB)+∠PDM$$

$$=∠DMP+∠DPM+∠PDM-∠DPB$$

$$=180°-90°=90°.$$

Therefore, $DM$ and $ME$ are orthogonal.

$ $