From a point $P$ in the given angle $∠XAY$, drop perpendicular lines $PQ$ and $PR$ to $AX$ and $AY$.

If $m$ is a positive constant, then the point $P$ is on a fixed line segment such that $PQ+PR=m$.

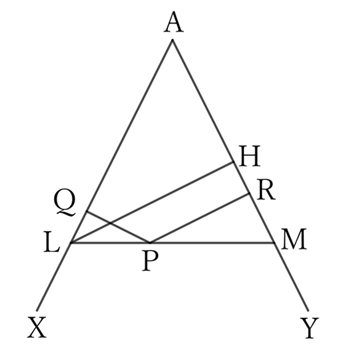
Draw a line that passes through $P$ and intersects $AX$ and $AY$ at points $L$ and $M$ such that $∠ALM=∠AML$.
Furthermore, if a perpendicular line $LH$ is dropped from $L$ to $AY$, from the problem $0151$,

$$PQ+PR=LH.$$
Therefore, $LH=m$, and since $LH$ must be a constant, the position of $L$ is fixed.
Thus, the isosceles triangle $ALM$ is a fixed triangle and the base $LM$ is a fixed line segment.
Therefore, $P$ is on the fixed line segment $LM$.

$ $