In a triangle $ABC$, let $AC>AB$.

Let the perpendicular line from $B$ to $AC$ be $BH$.

Let the perpendicular lines from a point $P$ on $BC$ to $AB$ and $AC$ be $PE$ and $PD$, respectively. Then

$$PD+PE>BH.$$

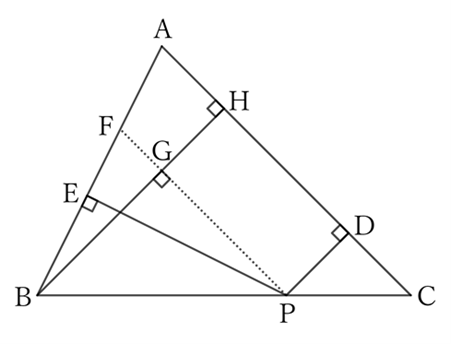
Draw a line parallel to $AC$ through $P$, and let $F$ and $G$ be the intersections of $AB$ and $BH$.

In$ △FBP$,

$$FP>FB. \qquad (∵ \ AC>AB)$$

Moreover, since $PE⊥BF$ and $BG⊥PF$, from the problem $0072$,

$$PE>BG,$$

$$∴ \ PE+PD>BG+PD,$$

$$∴ \ PE+PD>BG+GH, \qquad (∵ \ PD=GH)$$

$$∴ \ PD+PE>BH.$$

$ $