There are two lines that intersect at a point $Q$.

Now, on one of the lines, take three points $A, \ B$, and $C$ such that $QA=AB=BC$, and on the other line, take three points $L, \ M$, and $N$ such that $LQ=QM=MN$.

Then, the three lines $AL, \ BN$, and $CM$ intersect at a single point $P$.

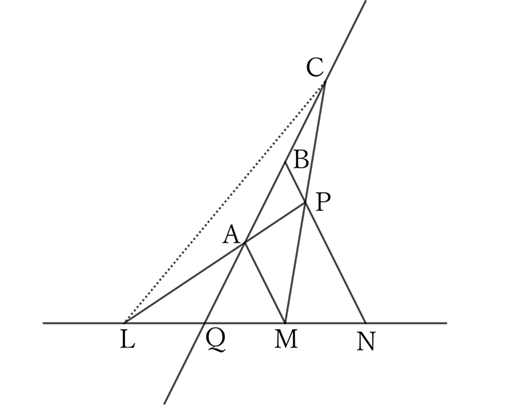
For $△CLM$,

$$LQ=QM.$$

Thus, $CQ$ is the median.

Moreover,

$$CA:AQ=2:1.$$

Therefore, $A$ is the center of gravity of $△CLM$.

Furthermore, for $△CAM$ and $△CBP$,

$$AM∥BP \qquad and \qquad CA∶CB=2∶1,$$

$$∴ \ △CAM∼△CBP,$$

$$∴ \ CM∶CP=2∶1.$$

Therefore, for $△CLM$,

$$CP=PM.$$

Thus, $LP$ is the median and passes through the center of gravity $A$.

Therefore, the three lines $AL, \ BN$ and $CM$ intersect at the point $P$.

$ $