Let the midpoints of sides $BC, \ CA$ and $AB$ of a triangle $ABC$ be $D, \ E$ and $F$, respectively.

Also, let $G$ and $H$ be the feet of perpendiculars drawn from $B$ and $C$ to any line passing through $A$, respectively, and $I$ be the intersection point of $EH$ and $FG$, or their extensions.

Then $∠EIF$ or its supplementary angle is equal to $∠EDF$.

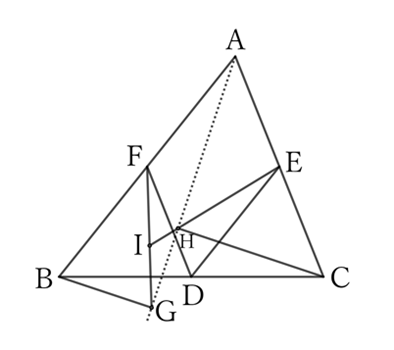
For right-angled triangles $ABG$ and $ACH$, $F$ and $E$ are the midpoints of the hypotenuses.

Thus, from the diagram above,

$$∠FGA=∠FAG. \qquad [1]$$

$$∠AHE=∠CAH,$$

$$∴ \ ∠IHG=∠CAH. \qquad [2]$$

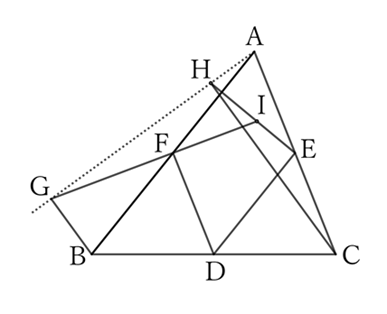
Or, from the diagram below,

$$∠CAH+∠ACH=∠R,$$

$$∠IHG=∠R+∠ACH, \qquad (∵ \ ∠EHC=∠ACH)$$

$$∴ \ ∠IHG=2∠R-∠CAH. \qquad [2]’$$

For the diagram above, if we add up $[1]$ and $[2]$,

$$∠FGA+∠IHG=∠FAG+∠CAH,$$

$$∴ \ ∠EIF=∠A.$$

However, since the quadrilateral $AEDF$ is a parallelogram,

$$∠A=∠EDF,$$

$$∴ \ ∠EIF=∠EDF. \qquad [3]$$

When $[1]$ and $[2]’$ are added together in the diagram below,

$$∠FGA+∠IHG=∠FAG+2∠R-∠CAH,$$

$$∴ ∠EIF=2∠R-(∠CAH-∠FAG),$$

$$∴ \ ∠EIF=2∠R-∠A.$$

However, since the quadrilateral $AEDF$ is a parallelogram,

$$∠A=∠EDF,$$

$$∴ \ ∠EIF=2∠R-∠EDF. \qquad [4]$$

From $[3]$ and $[4]$, $∠EIF$ is equal to $∠EDF$ or its complementary angle.

Conversely, $∠EIF$ or its complement is equal to $∠EDF$.

$ $