Let $O$ be any point inside a triangle $ABC$, and the midpoints of $AO, \ BO$ and $CO$ be $L, \ M$ and $N$ respectively.

Furthermore, if the midpoints of $BC, \ CA$ and $AB$ are $D, \ E$ and $F$ respectively, then the lines $DL, \ EM$ and $FN$ intersect at one point.

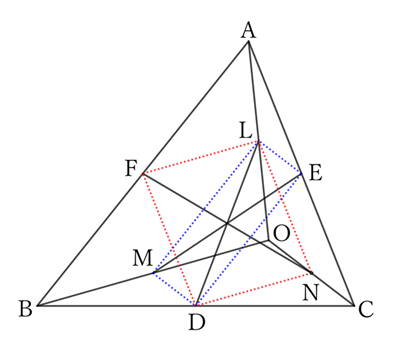
Since $L$ and $M$ are the midpoints of $AO$ and $BO$, respectively,

$$LM∥AB \qquad and \qquad LM=\frac{1}{2} AB.$$

Since $D$ and $E$ are the midpoints of $BC$ and $CA$, respectively,

$$ED∥AB \qquad and \qquad ED=\frac{1}{2} AB,$$

$$∴ \ LM∥ED \qquad and \qquad LM=ED. \qquad [1]$$

Similarly,

$$LE∥OC \qquad and \qquad LE=\frac{1}{2} OC.$$

Moreover,

$$MD∥OC \qquad and \qquad MD=\frac{1}{2} OC,$$

$$∴ \ LE∥MD \qquad and \qquad LE=MD. \qquad [2]$$

From $[1]$ and $[2]$, the quadrilateral $EDML$ is a parallelogram and its diagonal $EM$ intersects at the midpoint of $DL$.

Similarly, the quadrilateral $NDFL$ is a parallelogram and its diagonal $FN$ intersects at the midpoint of $DL$.

Therefore, the lines $DL,\ EM$ and $FN$ intersect at one point.

$ $