There is a circle inside a triangle.

Prove that the perimeter of the triangle is greater than that of the circle.

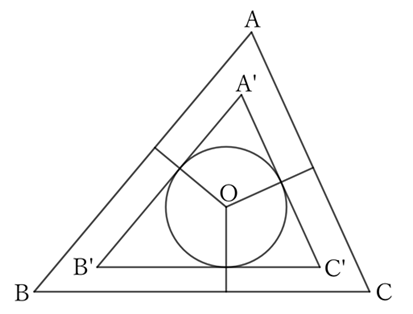
Create a triangle $A’B’C’$ that circumscribes the circle at the three points where perpendicular lines drawn from the center of the circle $O$ to the three sides of the triangle $ABC$ intersect the circle.

Since the triangle $A’B’C’$ is inside the triangle $ABC$,
$$AB+BC+CA>A’B’+B’C’+C’A’. \qquad [1]$$
Since the triangle $A’B’C’$ circumscribes the circle, it is clear that the area of the ​​triangle $A’B’C’$ is greater than that of the circle, and if the radius of the circle is $r$,
$$\frac{1}{2} r(A’B’+B’C’+C’A’ )>πr^2,$$
$$∴ \ A’B’+B’C’+C’A’>2πr. \qquad [2]$$
From $[1]$ and $[2]$,
$$AB+BC+CA>2πr.$$
In other words, the perimeter of the triangle is greater than that of the circle.

$ $