In the following $(1)$ to $(4)$, for the condition on the left about a quadrilateral,

if the condition on the right is a necessary and sufficient condition, answer $A$;

if it is a necessary but not sufficient condition, answer $B$;

if it is a sufficient but not necessary condition, answer $C$;

if it is neither a necessary nor sufficient condition, answer $D$.

     $(1)$ It is a trapezoid. $\quad – \quad$ A circle is inscribed on each of its four sides.

     $(2)$ The diagonals bisect each other. $\quad – \quad$ It is a rectangle.

     $(3)$ It is an isosceles trapezoid. $\quad – \quad$ The diagonals are of equal length.

     $(4)$ It is a parallelogram with diagonals of equal length. $\quad – \quad$ It is a rectangle.

(1) Even if a quadrilateral is a trapezoid, a circle is not necessarily all four sides are not necessarily inscribed on each of its four sides, and a quadrilateral with a circle inscribed on all four sides is not necessarily a trapezoid. Therefore, the answer is

$$D.$$

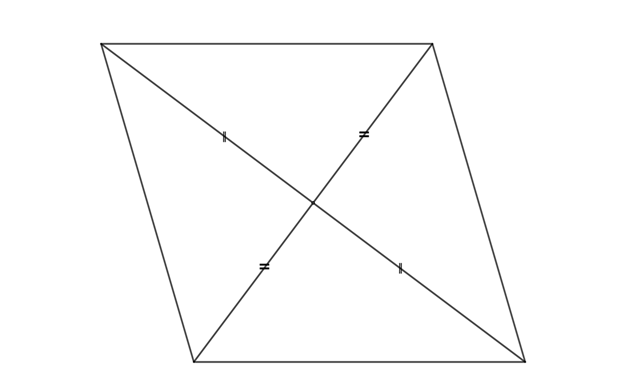
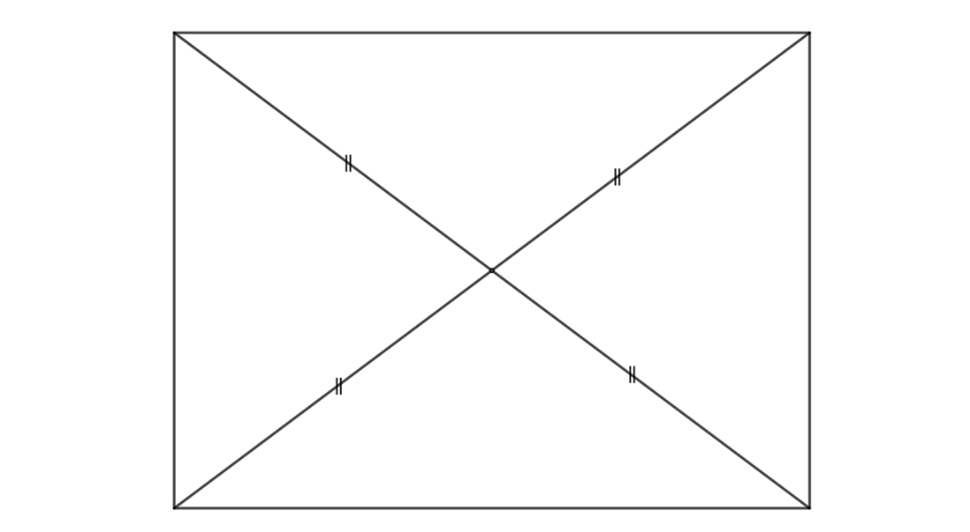
(2) A quadrilateral whose diagonals bisect each other is a parallelogram, but not necessarily a rectangle.
However, since a rectangle is a type of parallelogram, its diagonals bisect each other. Thus, the answer is

$$C.$$

(3) In an isosceles trapezoid, the diagonals are equal in length, but quadrilaterals with equal diagonals are not limited to isosceles trapezoids. Accordingly, the answer is

$$B.$$

(4) A parallelogram whose diagonals are the same length is a rectangle, and if it is a rectangle, the diagonals are all the same length. Hence, the answer is

$$A.$$