Problem
Let $ABCD$ be any quadrilateral, and let there be an interior point $O$ which is not the intersection of the diagonals; then the sum of $OA, \ OB, \ OC$ and $OD$ is greater than the sum of both diagonals $AC$ and $BD$:
$$OA+OB+OC+OD>AC+BD.$$
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
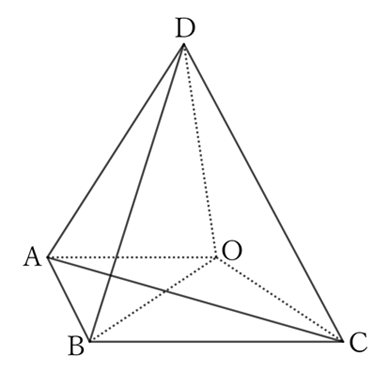
For $△OAC$,
$$AC<OA+OC. \qquad [1]$$
For $△OBD$,
$$BD<OB+OD. \qquad [2]$$
From $[1]$ and $[2]$,
$$AC+BD<OA+OB+OC+OD.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.42.