Problem
When the bisectors of the four angles of a quadrilateral pass through the same point, the sum of the lengths of one pair of opposite sides of the quadrilateral is equal to the sum of the lengths of the other pair of opposite sides.
$$ $$
$$ $$
$\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$ $\downarrow$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
$$ $$
Solution
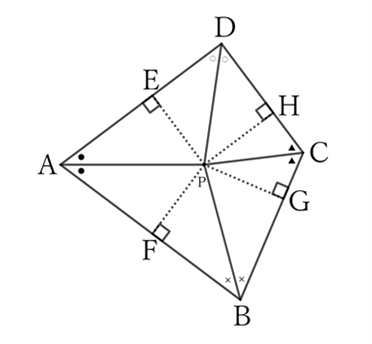
Right-angled triangles $PAE$ and $PAF$ share $PA$,
$$∠PAE=∠PAF \qquad and \qquad ∠PEA=∠PFA=∠R,$$
$$∴ \ ⊿PAE≡⊿PAF,$$
$$∴ \ AE=AF=a.$$
Similarly,
$$⊿PBF≡⊿PBG,$$
$$∴ \ BF=BG=b.$$
$$⊿PCG≡⊿PCH,$$
$$∴ \ CG=CH=c.$$
$$⊿PDH≡⊿PDE,$$
$$∴ \ DH=DE=d.$$
The sum of a pair of opposite sides $AB$ and $CD$ is
$$AB+CD=(AF+BF)+(CH+DH)=a+b+c+d. \qquad [1]$$
The sum of another pair of opposite sides $BC$ and $DA$ is
$$BC+DA=(BG+CG)+(AE+DE)=a+b+c+d. \qquad [2]$$
From $[1]$ and $[2]$,
$$AB+CD=BC+DA.$$
$ $
$ $
$ $
Reference Teiichiro Sasabe (1976) The Encyclopedia of Geometry (2nd edition), Seikyo-Shinsha, p.42.