The lines joining the midpoints of two pairs of opposite sides of a quadrilateral intersect at the midpoint of the line segment joining the midpoints of the two diagonals.

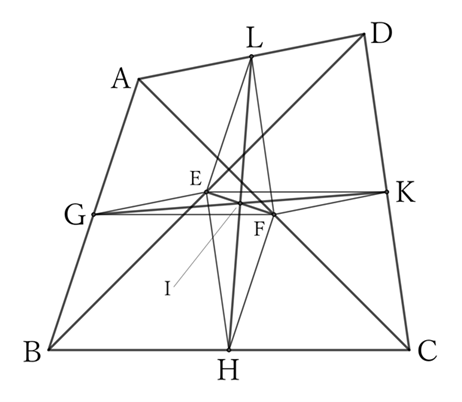
Let the midpoints of $AB, \ BC, \ CD, \ DA, \ BD$ and $AC$ be $G, \ H, \ K, \ L, \ E$ and $F$, and the midpoint of $EF$ be $I$.

$△BDA$ and $△BEG$ share $∠ABD \ (=∠GBE)$,

$$AB∶GB=BD∶BE=2∶1,$$

$$∴ \ △BDA∼△BEG,$$

$$∴ \ DA∶EG=2∶1,$$

$$∴ \ EG=\frac{1}{2} DA. \qquad [1]$$

$△CDA$ and $△CKF$ share $∠ACD \ (=∠FCK)$,

$$AC∶FC=CD∶CK=2∶1,$$

$$∴ △CDA∼△CKF,$$

$$∴ \ DA∶KF=2∶1,$$

$$∴ KF=\frac{1}{2} DA. \qquad [2]$$

From $[1]$ and $[2]$,

$$EG=KF. \qquad [3]$$

Similarly,

$$GF=EK. \qquad [4]$$

From $[3]$ and $[4]$, since the quadrilateral $EGFK$ is a parallelogram, its diagonal $GK$ passes through the midpoint $I$ of the other diagonal $EF$.

Similarly, since the quadrilateral $EHFL$ is a parallelogram, its diagonal $HL$ passes through the midpoint $I$ of the other diagonal $EF$.

Therefore, the lines $GK$ and $HL$, connecting the midpoints of two pairs of opposing sides of the quadrilateral $ABCD$, intersect at the midpoint $I$ of the line segment $EF$, which connects the midpoints of the two diagonals $AC$ and $BD$.