A necessary and sufficient condition for a quadrilateral $ABCD$ to be a parallelogram is that for any point $P$ in the quadrilateral, the following holds:

$$△PAB+△PCD=\frac{1}{2}◻ABCD. \qquad [*]$$

Show that this condition is necessary and sufficient.

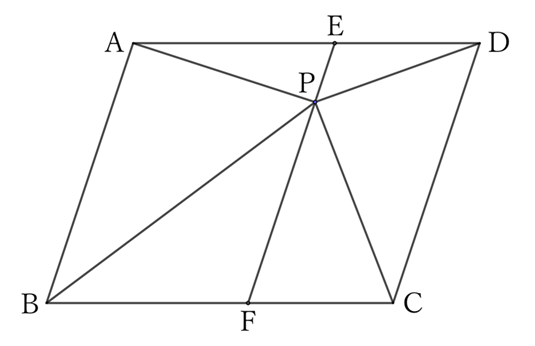
$(1)$ Necessary condition

Let the quadrilateral $ABCD$ be a parallelogram, and the points $E$ and $F$ are where the line that passes through $P$ and is parallel to $AB$ intersects with $DA$ and $BC$.

Then, since $EF$ is also parallel to $CD$, and both $◻ABFE$ and $◻CDEF$ are parallelograms,

$$◻ABCD=◻ABFE+◻CDEF,$$

$$△PAB=\frac{1}{2}◻ABFE \qquad and \qquad △PCD=\frac{1}{2}◻CDEF,$$
$$∴ \ △PAB+△PCD=\frac{1}{2} (◻ABFE+◻CDEF),$$
$$∴ \ △PAB+△PCD=\frac{1}{2}◻ABCD.$$

$(2)$ Sufficient condition
Assume $[*]$.
Then, for any quadrilateral $ABCD$, no matter where $P$ is located on $EF$ drawn parallel to $AB$, the area of $​​△PAB$ is always constant.
However, from $[*]$, $△PAB+△PCD$ is always constant.

Thus, the area of ​​$△PCD$ is also always constant.

Therefore,
$$EF∥CD,$$
$$∴ \ AB∥CD. \qquad [1]$$

Similarly,
$$DA∥BC. \qquad [2]$$

From $[1]$ and $[2]$, if $[*]$, then the quadrilateral $ABCD$ is a parallelogram.