If the midpoints of opposite sides $AB$ and $DC$ of a parallelogram $ABCD$ are $E$ and $F$ respectively, then $DE$ and $BF$ trisect the diagonal $AC$.

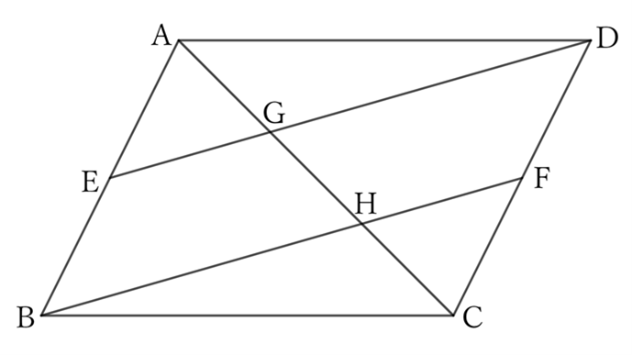
Since $AB∥DC$,
$$EB∥DF.$$
Also, since $AB=DC$ and $E$ and $F$ are the midpoints of $AB$ and $DC$, respectively,
$$EB=DF.$$
In other words, the quadrilateral $EBFD$ is a parallelogram.
Therefore,
$$BF∥DE.$$
For $△ABH$ and $△AEG$,
$$∠ABH=∠AEG, \qquad ∠AHB=∠AGE \qquad and \qquad AB∶AE=2∶1,$$
$$∴ \quad △ABH~△AEG,$$
$$∴ \quad AH∶AG=2∶1,$$
$$∴ \quad AG=GH. \qquad [1]$$
For $△CDG$ and $△CFH$,
$$∠CDG=∠CFH, \qquad ∠CGD=∠CHF \qquad and \qquad CD:CF=2:1,$$
$$∴ \quad △CDG~△CFH,$$
$$∴ \quad CG∶CH=2∶1,$$
$$∴ \quad CH=HG. \qquad [2]$$
From $[1]$ and $[2]$,
$$AG=GH=HC.$$
In other words, $DE$ and $BF$ trisect the diagonal $AC$.