If the midpoints of sides $CD$ and $AD$ of a parallelogram $ABCD$ are $E$ and $F$ respectively, then $BE$ and $BF$ trisect the diagonal $AC$.

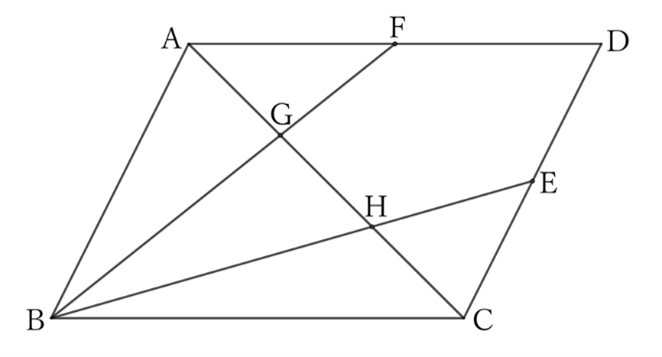
For $△HAB$ and $△HCE$, $$∠AHB=∠CHE \qquad and \qquad ∠HAB=∠HCE,$$ $$∴ \quad △HAB∼△HCE.$$ Also, since $AB∶CE=2∶1$, $$HA∶HC=2∶1. \qquad [1]$$ Similarly, for $△GBC$ and $△GFA$, $$∠BGC=∠FGA \qquad and \qquad ∠GBC=∠GFA,$$ $$∴ \quad △HAB∼△HCE.$$ Also, since $BC∶FA=2∶1$, $$GC∶GA=2∶1. \qquad [2]$$ From $[1]$ and $[2]$, $$AG∶GH∶HC=1∶1∶1.$$ In other words, $BE$ and $BF$ trisect the diagonal $AC$.